3.分子が分母の微分した形の場合 分子が分母を微分したような形になっている場合も置換積分を省略することができます。 1で説明したカッコ・ルートの中身が被積分関数に含まれている場合の、カッコの外が 1 乗のパターンとおなじです。 分数式の積分は,公式 $\displaystyle\int\cfrac{1}{x}\space dx=\log xC$ より,$\log$ に直していきます。 しかし,この式は分母が複雑で,合成関数を考えながら積分するのはかなり難しそうです。 分数階微分作用素 このような理論の存在については、12年からのリウヴィルの論文にその素地を見ることができる。 函数の階数 a の分数階微分は今日ではしばしばフーリエ変換あるいはメリン変換といった積分変換の意味で定義される。

单变量微积分笔记23 部分分式 我是8位的 博客园
分数 微分 分母 定数
分数 微分 分母 定数- 微分演算子を使うといろいろな「公式」が生まれるのでそれを工夫して適用すれば比較的簡単に求められます。 まず Dの式は普通の多項式のように扱うことができます。 (Da)(Db)=(Db)(Da)とか部分分数分解とかそういうのが普通にできます。 分数関数の積分の解法 Point:分数関数の積分 (1) 分子が分母を微分した式 のとき、 (2) 分子の次数 > 分母の次数 分子を分母で割った式より、分数式を分けて積分します。 例えば、 (3) 部分分数に分ける これらの式を用いて、部分分数に分けて積分します



本的质基性比上海市傅雷中学樊丽华 1 分数的基本性质 分数的分子和分母同时乘以或除以相同的数 0 除外 分数的大小不变 填空 Ppt Download
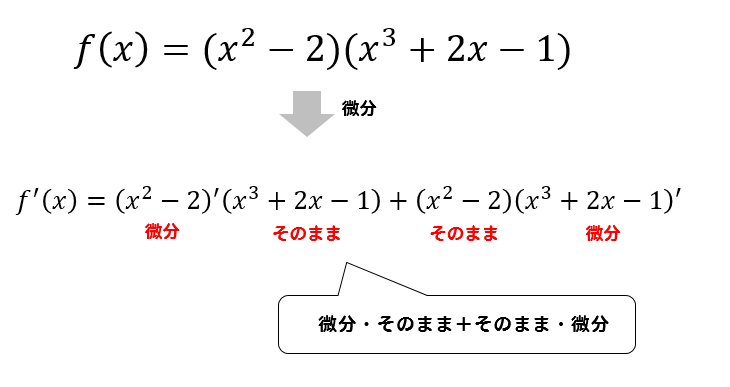
分数関数の微分を秒速で終わらせるテクニック 解決するためのステップは、 たったの3つ ! STEP1 分数をべき乗関数に直す を として、表現を改めます。 STEP2 積の微分公式 を適用 「微分そのまま+そのまま微分」 を行います。 STEP3微分積分 dy/dxを求める x^ (1/3)y^ (1/3)=1 x1 3 y 1 3 = 1 x 1 3 y 1 3 = 1 方程式の両辺を微分します。 d dx (x1 3 y1 3) = d dx (1) d d x ( x 1 3 y 1 3) = d d x ( 1) 方程式の左辺を微分します。 タップしてもっと手順を表示する 総和則によって x 1 3 y 1 3 x 1 3 y 1 3 を x x に 分数の分母にゼロがくることは許されていません。 しかし、極限の計算においては、 0/0ができてしまう場合があるのです。 先程、dxやdyは定義できないと書きましたが、 むりやり書くことはできます。
この操作のことを「\(\dfrac{1}{4×5}\) を部分分数分解する」と言います。 微分や積分など、複雑な計算をするときは部分分数分解で「分数の足し算」に変形すると計算が楽になるケースが少なくありません。 部分分数分解をマスターすると、そういった複雑な計算でつまずく事がグッと 方法/步骤 我们先打开一个需要插入分数的ppt,看文档的左上角,有一个"插入",点击它。 点开的"分数模板"中,有上下两分,上面填分子,下面填分母。 然后关闭"公式编辑器",这时,分数就出现在ppt上了。 在分数周围,有8个小白点,是用来调整分母に変数があるときの最大値・最小値の問題を2通りの方法で解説しました 問題 のとき、関数 の最大値を求めよ。 注意 かなりの長文です。 1回ではなかなか理解できません。 2回、3回と繰り返し読めば言わんとしていることが分かってくると
分数も当然、割り算の形で表せるということになります。 このように 分数は上 (分子)÷下 (分母)で表すことができます。 この考え方から 分母と分子が分数になったとしても このように計算できるというわけです。 この計算に慣れてきた人は、この 分数怎么求导 狮子tuojie 06 例题详解 1 /5 分步阅读 例题求函数的导,例题如下图 图 2 /5 第一步将函数分成分子函数,分母函数两个部分,如下图所示611 有理関数の積分 ~ 部分分数の積分 被積分関数の有理式の分母が 0 となるのは のときだから, 代数方程式 を複素解も含めて解くと, となる. 複素解を順に , , , とおくと, 分母は と因数分解される. 被積分関数の有理式を部分分数分解すると,




复合函数求导求到什么时候才算完啊 分子分母都是带分子分母都是复合函数




高等数学 11 泰勒公式求极限 第三章微分中值定理 每日头条
微分積分 ii 81 分数関数を積分する時は 要点まとめ 分数関数を積分する時は, まず分子の次数を下げられないか考える。 分母が因数分解できるなら, 因数分解し, 部分分数に分ける。 分数 \frac{ }{ } 第一个{ }写分子,第二个{ }写分母。 名称 数学表达式 markdown公式 分数 $\frac{a1}{b1}$ 累加 \sum_{ }^{ } 累加号的上标下标的前后顺序可以互换。 名称 数学表达式 markdown公式 求和号 $\sum{x^n}$ 带范围求和分子 1 の微分は 0,分母 x2 の微分は 1 だから




人教版六年级上册数学全册知识点梳理 楠木轩




分数短除法 大熊 Csdn博客
同次形微分方程式 さて,次の問題は どのようなときに \(\displaystyle \frac{y}{x} = u\) の置き換えが有効か? です。 \(\displaystyle \frac{y}{x} = u\) の置き換えにより変数分離形に変形できる微分方程式を 同次形微分方程式 とよびます。 どのようにしたら,ある微分方程式が同次形であることを見抜ける 分数関数の積分は、式の形によって解き方を工夫する必要があります。 代表的なパターンを確認していきましょう。 ① 分子に分母の微分が隠れているパターン 分子に分母の微分の形があれば、次の積分公式を利用できます。 分母の微分が分数になる場合,\ 一気に「分子が分母の微分型」に気付きにくくなる 結果として,\ 分子にあるはずのものが分母にあることになるからである つまり,\ {1}{x(log x1)}\ を\ {1x}{log x1}\ とみなせるかが問われているわけである



将 汉字 用作 数学符号 是否可行



微積 微分 看板math Ptt網頁版
部分分数分解 分数式を分母の因数を分母にする幾つかの分数の和に変形すること。 有理関数の積分で用いられるために,積分可能な関数の和にする。この点については,微分積分/演習 で学ぶ。少し複雑に見えますが, 両辺の分母の形を頑張って覚えましょう。 1と2を覚えれば3も覚えられます。より一般的な形はヘビサイドの展開定理の定理1をどうぞ。 以下では,基本形をふまえて部分分数分解の方法( a, b, c a,b,c a, b, c の求め方)を3通り解説します。 方法1:分母を払って係数を 無理矢理微分形接触型に変形する解法が時としてかなり有効である 本解が正攻法である\ 分数関数の積分ではe^x1=tとすべきであったが,\ 本問ではほぼ意味がない e^x1=tのときdx= {dt} {e^x}= {dt} {t1}\ となり,\ {1} {e^x1}dx=1t {1} {t1}dt\ となるからである 分母が



导数思维导图高中 搜狗图片搜索




Cnb 一种基于分数阶偏微分方程的纹理图像高精度去噪滤波器 Google Patents
分数関数の微分iを参照) ホーム >> カテゴリー分類 >> 微分 >> 導関数の基本式I >>分数関数の微分II 最終更新日: 21年3月19日無理関数の微分公式は覚えても無駄 が紹介されているかもしれません。 しかしこの公式は覚えるよりも、 自分で導出したほうが絶対にラク なんです。 さえできれば、瞬殺できる問題だから。 さらに、平方根だけでなく3乗根以上でもOK。 なんでも暗記 絶対値の中が負になることはないので、最後に絶対値を外しています。 なお、 cosx ≠ 0 cos x ≠ 0 なので、 1 −sinx ≠ 0 1 − sin x ≠ 0 です。 標準不定積分の置換積分(三角関数) では「3乗を、2乗と1乗に分ける」という計算をしましたが、ここ




三角関数の微分 公式の証明と例題 高校生向け受験応援メディア 受験のミカタ



分数解方程加减 图片搜索
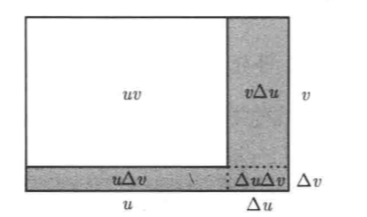
① 分母が単項式 ( 分数式は整式にして単項式ごとにみる(以前のプリント) ② 分母の微分 分母 ( 置換積分法で orj分母 (以前のプリント) ③ 分母が多項式で(分母の次数)<(分子の次数)( $ % 4 5 ④ 分母が因数分解可能 ( 部分分数分解7.いろいろな微分の公式 ~商の微分~ この章では商の微分を学びます。次のような関数が微分できるようになるのです! さて、このように分母に変数がある場合はどのように微分したらいいので6 函數相乘的微分 假設x 變化的增量為 x ,則應變量u, v 的變化分別為 u = f(x x) –f(x) v = g(x x) –g(x) 相乘函數的值便是(u u)(v v) ,在其值為正時,我們剛好可以用前面圖一的矩形面積來表示。 此時矩形面積的變化即為:



2 7 分数的加法和减法 51cto Com
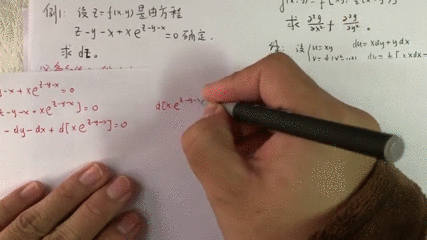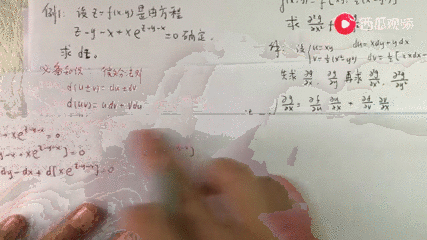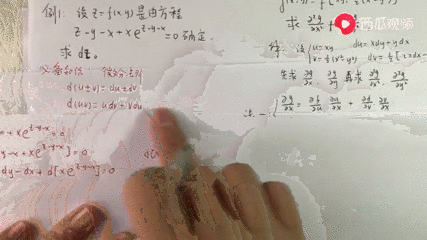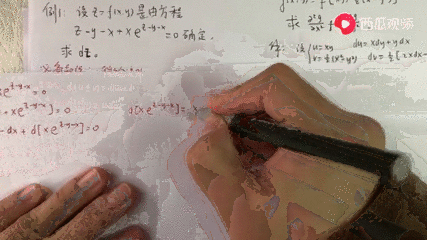



分数求偏导数的公式 搜狗搜索



异分母分数加 减法 Ppt Download




分子分母求导公式 分子分母都含有x 导数怎么求 三人行教育网 Www 3rxing Org




多項式的微積分 维基教科书 自由的教学读本




分数怎么化成带分数 人教版五年级数学下册4 4假分数化成整数或带分数的方法知识点 微课堂 图文解读 立志变强的人的博客 Csdn博客




高等数学 分母阶数未知 如何对分子进行泰勒展开 对泰勒公式展开阶数问题的分析 寒泉 程序员宅基地 程序员宅基地




求不定积分时可不可以将被积函数的分子分母同乘一个含有积分变量的式子f X 而f X 在某个点等于0 雨露学习互助




大学分式拆项公式 高数中拆项分式法 三人行教育网 Www 3rxing Org




异分母分数加 减法 Ppt Download



一元函数全微分公式 一元函数的微分excel函数公式大全哪儿呢 房产新闻 答辩网



微分和积分转换公式 Cos和sin转换公式积分公式哪里人啊 房产新闻 答辩网




Cnb 一种基于分数阶偏微分方程的纹理图像高精度去噪滤波器 Google Patents




P4 同分母分數加減混合計算 1 Chusir Youtube



分式函数积分 分母是根号内二次函数怎么办 哔哩哔哩 Bilibili




Latex 分数和二项式 Maimang1001的专栏 Csdn博客 Latex 分数
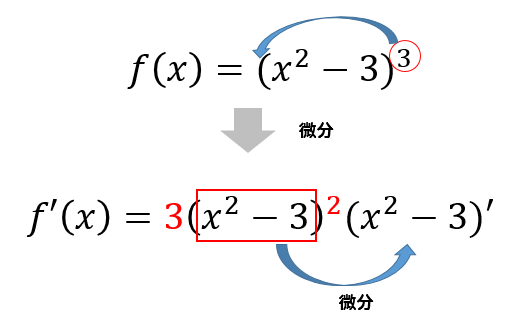



微分のやり方 計算方法まとめ 分数や三角関数のやり方は 数スタ




同分母分数加 减法分数的初步认识绿色圃中小学教育网 Ppt Download




高等数学 11 泰勒公式求极限 第三章微分中值定理 每日头条



科学网 Zmn 03 薛问天 对 反函数导数定理 的严重歪曲 评师教民先生 0199 文清慧的博文



3




高校数学 微分形接触型の一種 分子が分母の微分型 置換せずに瞬殺せよ 受験の月




分母微分分母的微分如何計算 百度知道狀態 Trtv



Http Blog Ncue Edu Tw Sys Lib Read Attach Php Id




請問這題怎麼微分 Clear




异分母分数加 减法 Ppt Download




分数関数の微分について Den Of Hardworking



考研二战统计学学硕复习blog数学篇第八天 教育资讯 电影风云娱乐网



数 微分法 数学用語解説




单变量微积分笔记23 部分分式 我是8位的 博客园




分数模型 新人首单立减十元 21年8月 淘宝海外



陪你复习微积分 六 求解微分问题 知乎



Http Www Bannedthought Net China Magazines Dialecticsofnature Dialecticsofnature 1974 02 Ocr Pdf




本的质基性比上海市傅雷中学樊丽华 1 分数的基本性质 分数的分子和分母同时乘以或除以相同的数 0 除外 分数的大小不变 填空 Ppt Download




第一为什么2 5化分母不是4分之一吗 为什么成5分之2 怎么化的 还有下面的根号169哪来的4哪来的第二题




微分 分数関数の微分 大人が学び直す数学




矩阵微积分 二 Xiaomeng29的博客 程序员宅基地 矩阵积分 程序员宅基地




I1 Kknews Cc Sig 3fi075c 4nss144q366o Jpg




高等数学 11 泰勒公式求极限 第三章微分中值定理 每日头条




微分公式分母3 Gxplu



分数解方程加减 图片搜索



指数幂微分 指数函数 分数指数幂 尚书坊




分数模型 新人首单立减十元 21年8月 淘宝海外




Cnb 一种基于分数阶偏微分方程的纹理图像高精度去噪滤波器 Google Patents




B 28 基本的微分公式 求导的利器 重点 知乎




部分分式積分法三 Youtube



微积分学 维基百科 自由的百科全书



分数関数の不定積分




异分母分数加 减法 Ppt Download




分母微分分母的微分如何計算 百度知道狀態 Trtv




分母微分分母的微分如何計算 百度知道狀態 Trtv




微分公式六 分式微分及其實例 Youtube



科学网 Zmn 09 师教民 评 对 反函数导数定理 的严重歪曲 评师教民先生的 0199 文清慧的博文




微分积分简要总结 简书




分数的微分怎么求 搜狗搜索




异分母分数加 减法 Ppt Download



微分のやり方 計算方法まとめ 分数や三角関数のやり方は 数スタ




Cnb 一种基于分数阶偏微分方程的纹理图像高精度去噪滤波器 Google Patents




同分母分数加 减法分数的初步认识绿色圃中小学教育网 Ppt Download



B 28 基本的微分公式 求导的利器 重点 知乎




同分母分数加 减法分数的初步认识绿色圃中小学教育网 Ppt Download




例題 根式的化簡 分數型 Youtube



異分母分數加法 Geogebra




异分母分数加 减法 Ppt Download




数学の質問です 分数関数の分母に二乗がついていた場合はどのように計 数学 教えて Goo



偏微分符号怎么输入




本的质基性比上海市傅雷中学樊丽华 1 分数的基本性质 分数的分子和分母同时乘以或除以相同的数 0 除外 分数的大小不变 填空 Ppt Download
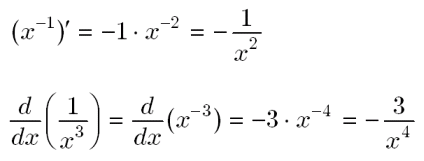



微分 分数関数の微分 大人が学び直す数学
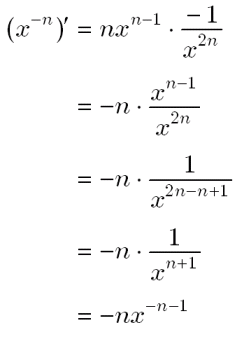



微分 分数関数の微分 大人が学び直す数学



72道积分题略详解析 31 50 知乎




Limit
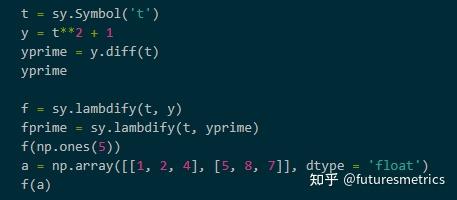



再谈数值微分 知乎



指数幂微分 指数函数 分数指数幂 尚书坊



科学网 Zmn 0199 师教民 评 欲盖弥彰真相大白 师教民先生的 0191 文清慧的博文




大一上学期 高等数学 知识整理 第四章不定积分 哔哩哔哩




单变量微积分笔记23 部分分式 我是8位的 博客园
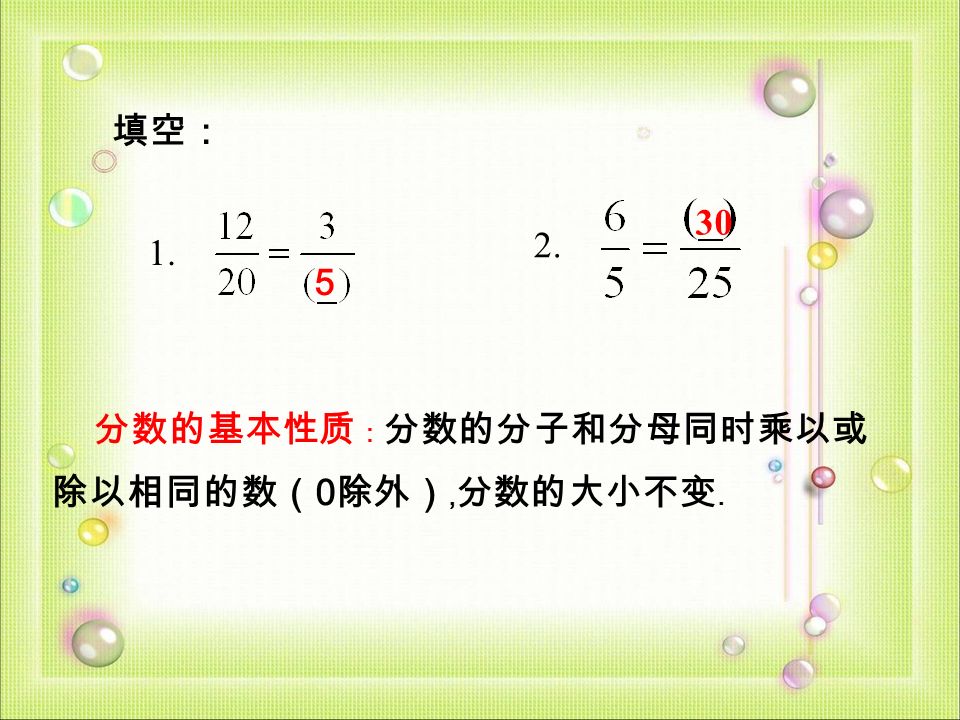



本的质基性比上海市傅雷中学樊丽华 1 分数的基本性质 分数的分子和分母同时乘以或除以相同的数 0 除外 分数的大小不变 填空 Ppt Download



指数幂微分 指数函数 分数指数幂 尚书坊




分子分母公式 异分子分母乘法三阶魔方公式图解哪儿看呢 龙口资讯门户网站




微积分小卡片 一本书到一张卡 每日头条



指数幂微分 指数函数 分数指数幂 尚书坊



偏微分教えてください Z Y Xのx微分とy微分を求めたいです 途中計算も Yahoo 知恵袋



無理関数の導関数




怎么计算分数除以整数 生活百科



指数幂微分 指数函数 分数指数幂 尚书坊




人教版六年级上册数学全册知识点梳理 楠木轩




不定积分 分子分母次数较高 Lhwjgs的博客 Csdn博客



下記の微分の問題ですが 分数を微分する時の公式 分母が2乗される を使おうと思 Yahoo 知恵袋



3 6連鎖律



B 28 基本的微分公式 求导的利器 重点 知乎




数学 の微分の問題です 4 の関数を微分する問題がわかりません 途 数学 教えて Goo



0 件のコメント:
コメントを投稿