三平方の定理を使うと、直角三角形の 2 つの辺の長さからもう一つの辺の長さを求めることができます。 このページでは、三平方の定理を分かりやすく説明しています。中学校で学習する前の人にも、三平方の定理の意味を理解してもらえるような解説にしているので、ぜひお読みください。三平方の定理で辺の長さ,高さや表面積,体積,最短距離を求める問題 印刷機能有 koya7シリーズ ソフト詳細説明 このソフトは,マイクロソフト VisualBasic19で作成したもので,実行ファイル(exe)になっており,三平方計算21exeをクリックすれば起動できます。まとめ1(展開,因数分解,根号) まとめ2(2次方程式,解の公式,文字係数) まとめ3(三平方の定理,辺の比が分かっている三角形,空間図形) まとめ4(素数,最大公約数,最小公倍数,整数問題) まとめ5(平行線と線分の比,相似比) まとめ6(2次関数,変化の割合,放物線と直線)

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
三平方の定理 表面積
三平方の定理 表面積-三平方の定理6 2 1辺3㎝の正四面体の体積と表面積を求めよ。 表面積 1辺3cmの正三角形の面積を出す。 頂点aから辺bcに垂線amを引くと abmは30°、60°、90°の直角三角形となる。 ab=3なのでabam=2 3 より am = 3 3 2 これが abcの高さなので 面積 abc = 3× 3 3 2 ÷2= 9 3 4数学37章三平方の定理「三平方の定理の利用」<基本問題①> 組 番 名前 1次の図形の対角線の長さを求めなさい。 (1)縦,横の長さがそれぞれ4㎝, ㎝の長方形 (2)1辺の長さが7㎝の正方形 22点A(-3,2),B(1,-3)が




三平方の定理 自動計算サイト
三平方の定理覚えておきたい基本公式を解説! 三平方の定理 131 直方体、立方体の対角線の長さは公式でラクラク計算できるぞ!三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し(2)三平方の定理のいろいろな証明を理解させる。 (3)三平方の定理を利用して,直角三角形の未知の辺の長さを求めることができるように する。 (4)三平方の定理の逆を理解して,三角形が直角三角形であるかどうかを判断することが できるようにする。
単元 立体の体積と表面積, 「75°、15°、90°の辺の比など、教科書には載っていない便利な定理・公式です。 実際に高校受験のときによく使っていました。 覚えておくとかなり役に立ちます。」, 学年 中学3年生, キーワード 三平方の定理,相似な図形,円の接線,内接円,外接円,正三角形,正三平方の定理応用(錐の表面積・体積) 次のそれぞれの立体の体積と表面積を求めよ。 底面の半径3cm, 母線の長さ5cmの円錐 5cm 3cm 体積 表面積 一辺6cmの正四面体 6cm 体積 表面積 底面が一辺10cmの正方形で、その他の辺がすべて13cmの正四角錐 13cm 10cm 体積 表面積表:1)三平方の定理を利用して、直角三角形の未知の辺の長さを求めることができる。( (2)三平方の定理の逆を使って、三角形が直角三角形であるかどうかを判断することができる。 知:1)三平方の定理やその逆を理解する。( 2節
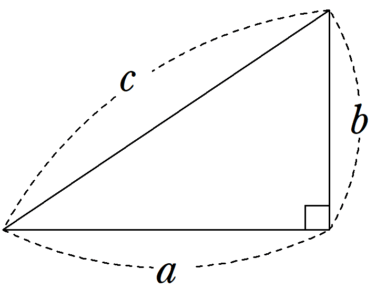
三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




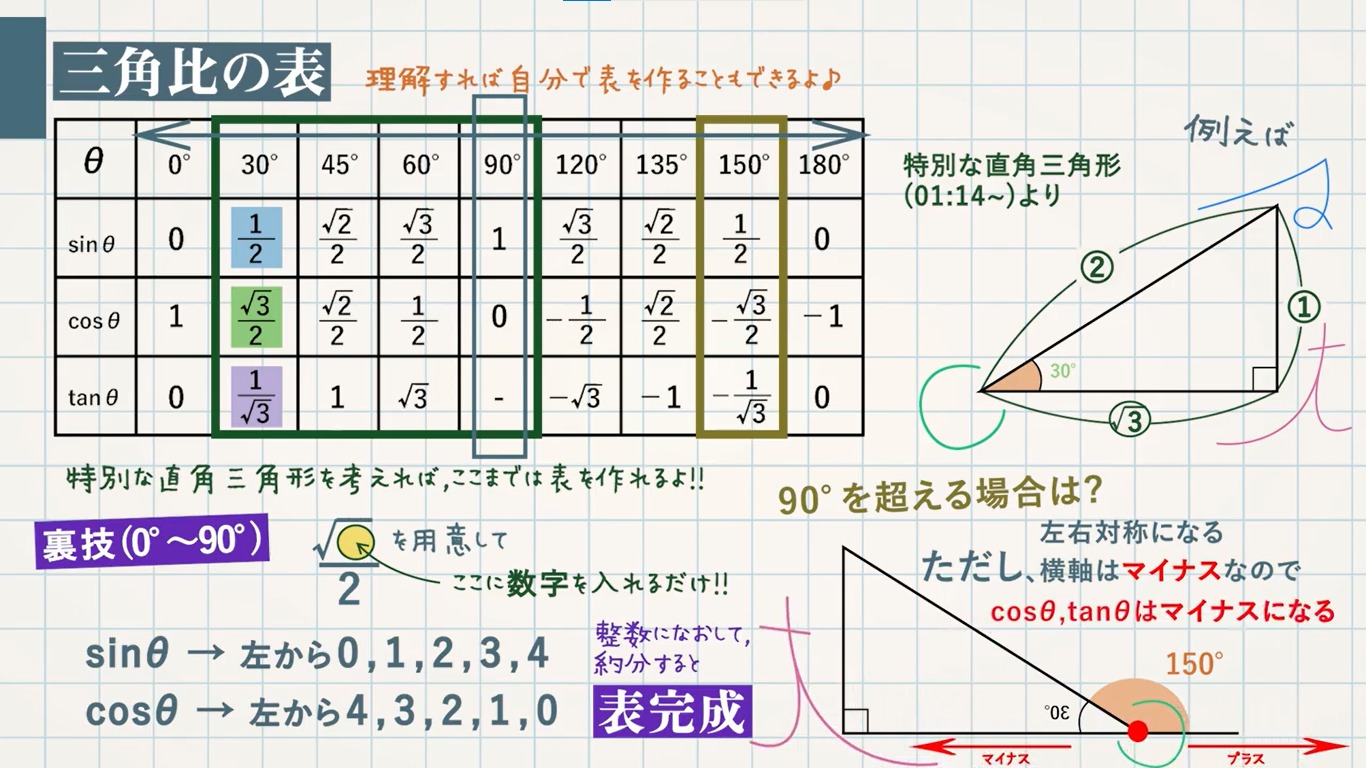
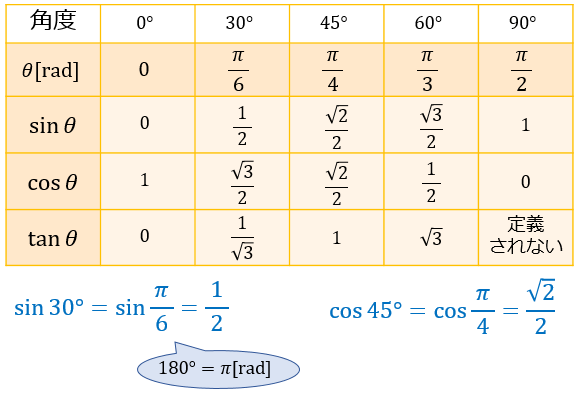
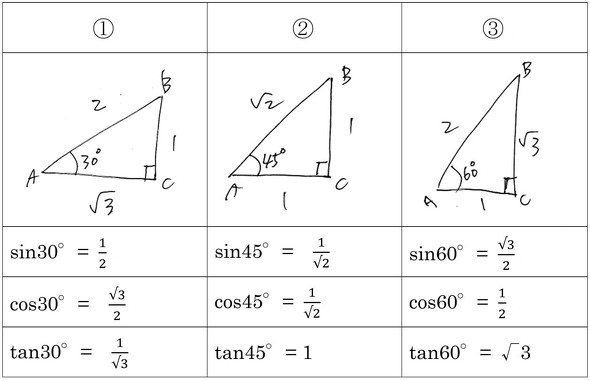
三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学
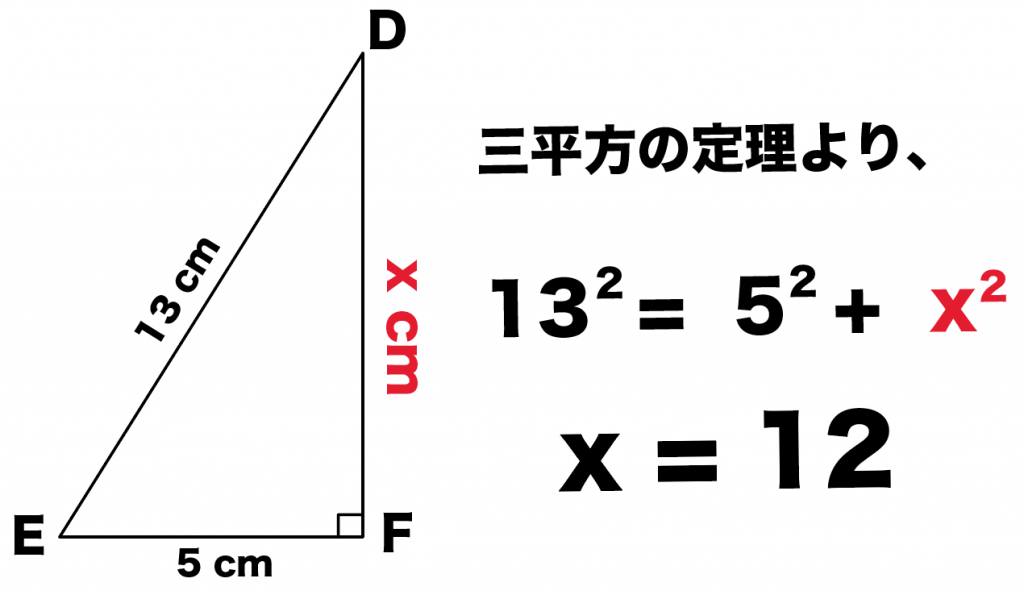
母線= 半径×中心角中心角半径= 母線× 360° 半径中心角=360×母線実施時期 3年生2学期(12月) 単元項目 7章1節 三平方の定理(p198) 配当時数 3時間 指導内容 三平方の定理の発見とその性質三平方の定理でACを出す。 x2 = 2212 x2=5 x>0よりx= 5




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



2
初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦の定理(こうカーナビはなぜ正確なの? その秘密、「三平方の定理」で教えます 折り紙を使った簡単な証明も! 動画あり 横山 明日希 プロフィール また表会をする(12・13校時) 5 本時の学習 (1) ねらい 既習事項を使って,三平方の定理を証明するための構想・見通しを立てることができる。 (2) 展開 主な学習場面と子どもの取組 教師の支援と願い・評価 1.三平方の定理を確認する。



3



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
三平方の定理を知る 29 11/22 三角定規の性質 30 11/29 三平方の定理の利用 31 12/6 正多面体 32 12/13 場合の数から確率へ 順列 33 12/中3数学 第7章 三平方の定理 学習プリントNo1 今日のPoint 1 三平方の定理を見いだそう。 1 教科書P180 直角三角形を教科書に書こう。 →角の大きさは 2 教科書P181 図形のしきつめに挑戦しよう。7章 三平方の定理 1.プリント ダウンロード レベル 1




三平方の定理から四立方の定理へ 東京図書出版




壁紙 押入れ トップ 100 三 平方 の 定理 表
三平方の定理を見いだすことができる 表直角三角形の直角をはさむ2辺の長さと斜辺の長さをそれぞ れ文字で表し,それを用いて三平方の定理を式に表すことが できる 知三平方の定理は,3辺の長さの関係を表すとともに面積の関方 の 定 理 1 三平方の定理の逆 3:4:5の長さの三角形やピタゴラス数に興味を もって追究しようとしている。 2 三平方の定理 三平方の定理が成り立つ理由がわかる。 3 たしかめ 三平方の定理を用いて辺の長さを求めることが できる。・三平方の定理の逆 方形のそれぞれの辺でできる三角形の形で 解することができる 判断できた理由を直角三角形の辺の関係か ら考えさせる 補助線を考え出して,直角三角形を見つける表三平方の定理を用いて,図形の辺 三平方の定理を利用する 操作活動




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




神奈川県公立高校入試 出題範囲 あすもりのブログ
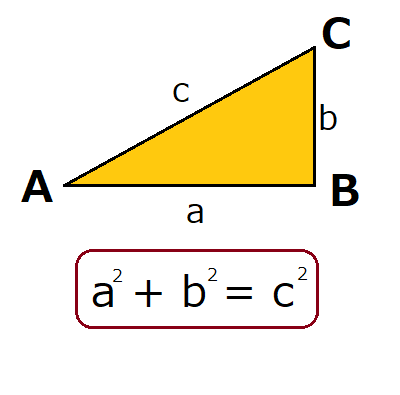
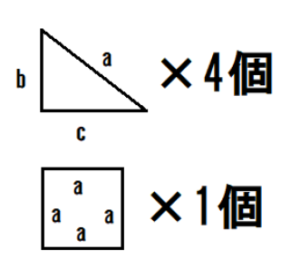
三平方の定理とは、次のような定理です。 三平方の定理(ピタゴラスの定理) 上のような直角三角形で、次の等式が成り立つ。 a2 b2 = c2 a 2 b 2 = c 2 直角三角形の2辺がわかれば、残りの1辺も求まるというもので、紀元前から測量等でも使われてきましたNo8 発展三平方の定理① 組 氏名 問1 直角三角形の斜辺の長さを ,他の2辺の長さを , とするとき,次の表を完成しなさい。 問2 次の図でxの値を求めなさい。 問3 AB=5cm BC=6cm CG=4cmの三平方の定理について理解し、それらを活用することができるようにする。 そのために、 ア.直角三角形の3つの辺の長さの関係を具体的な観察や操作を通して調べ、三平方 の定理を見いだす。 イ.三平方の定理が証明できることを理解する。




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




わかりやすい三角比と基本公式 Irohabook
三平方の定理 きる。 きる。 を用いて、空間 三平方の定理を 三平方の定理 図形の長さ、面 用いて、直方体のを用いて、直方 積、表面積や体 対角線の長さや立体の対角線の長 積などを求める 体の体積、表面積さや立体の体積、 ことができる。学習プリント画像をクリックすると問題が開きます。 解答が必要な場合は、下の一覧表の 解答(pdf) をクリックしてください。 一括(pdf) は 問題と解答 がセットでダウンロードできるようになっています。 練習問題とは、本研究委員会で作成した問題のことです。




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




二個の平方数の和 Wikipedia



1



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club




数学 中3 61 三平方の定理 基本編 Youtube




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



Http Www Nc Gunma Boe Gsn Ed Jp Action Common Download Main Upload Id 2510




都立入試数学 三平方の定理を使わなくても解けるか 都立に入る




壁紙 押入れ トップ 100 三 平方 の 定理 表




世界一わかりやすい数学問題集中2 3章 一次関数



三角関数とは コトバンク




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




高校受験21 福岡県立高校入試 学力検査の出題範囲を一部除外 リセマム




一次関数 表から式を求めるやり方についてイチから解説 Youtube



平方剰余と平方非剰余




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ



三平方の定理




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



勾配 斜長 法長 斜辺 換算表




これで解決 タープ テントのロープの長さガイド 計算方法をわかりやすく解説 3ページ目 暮らし の




三平方の定理 相似を利用した問題 問11の 2 を教えてください Clear
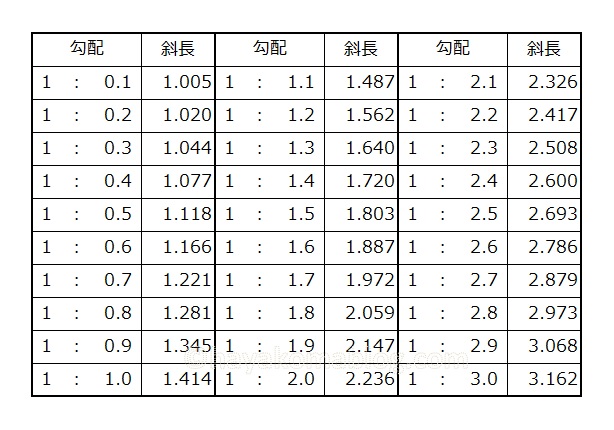



勾配 斜長 法長 斜辺 換算表




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 覚えておきたい基本公式を解説 数スタ
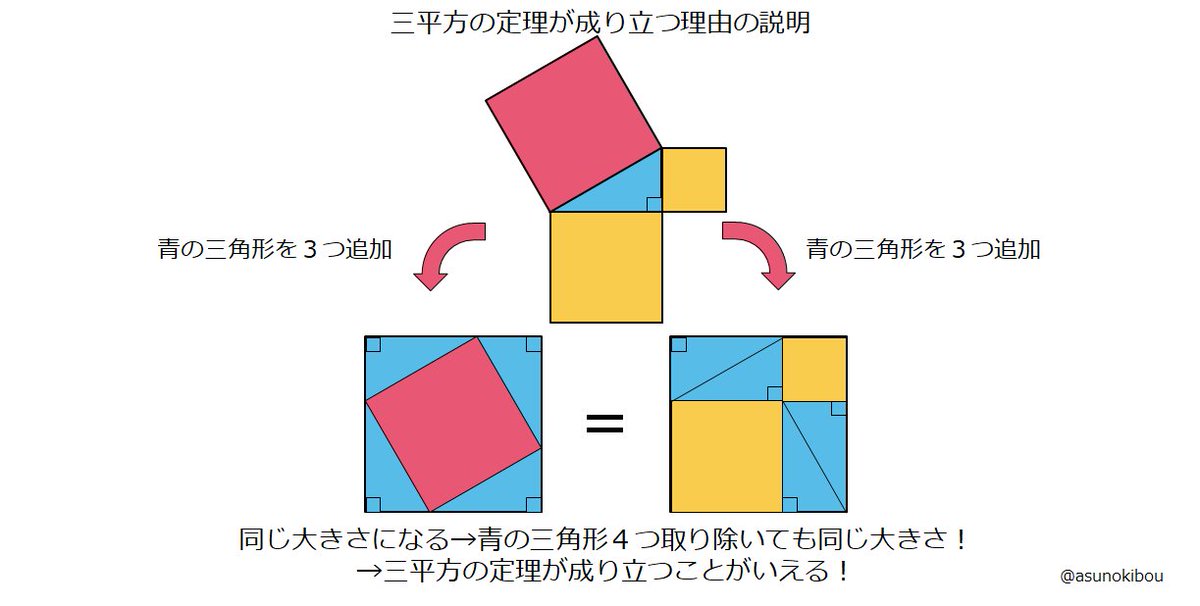



三平方の定理 ピタゴラスの定理 を分かりやすく表した動画 Togetter




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



3




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




教えてください Clear




三角比を考え方から理解する 有名角の三角比も説明
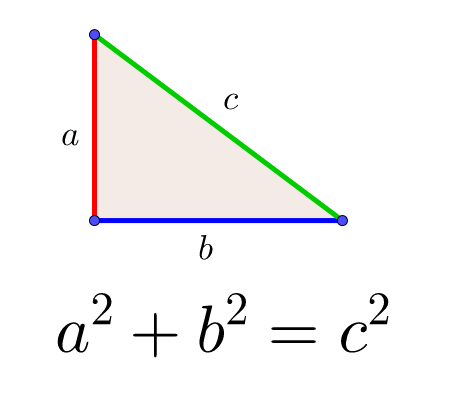



三平方の定理の証明4 直角三角形と内接円 キソカラ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ




ピタゴラス




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



2




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



印刷 三 平方 の 定理 表 ニスヌーピー 壁紙



Mathematics 三平方の定理 3 いろいろな三角形 働きアリ



3d Cadで設計の総仕上げ 動きや質感まで確認してみよう そして 次のdiyへ ステイホームでdiyを極める 玄人志向なモノづくり 4 4 4 ページ Monoist




ピタゴラスは遅かった 三平方の定理 最古の応用例 朝日新聞デジタル




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学




わかりやすい三角比と基本公式 Irohabook




高校数学 三平方の定理による三角関数の計算 1 映像授業のtry It トライイット



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会




コラム ピタゴラスの定理 江戸の数学




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




これで解決 タープ テントのロープの長さガイド 計算方法をわかりやすく解説 3ページ目 暮らし の



数学史3 7 バビロニアの数学 三平方の定理 Fukusukeの数学めも
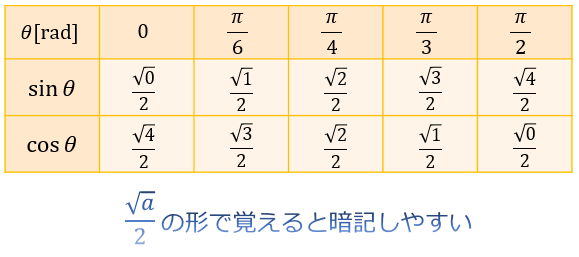



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ
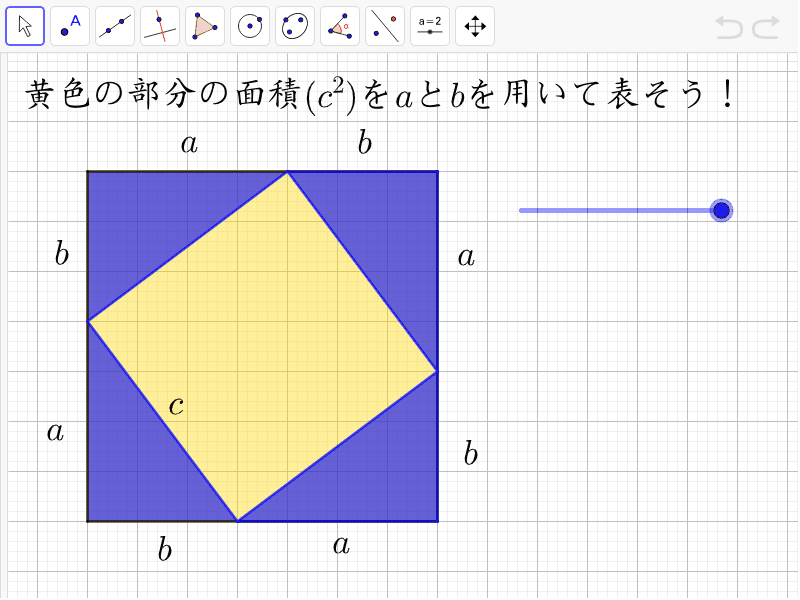



三平方の定理の証明 ピタゴラス Geogebra




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室




三平方の定理 自動計算サイト




わかりやすい三角比と基本公式 Irohabook



証明にこだわる




ピタゴラスの定理 三平方の定理 ベクター イメージマート



三平方の定理によりabが5だったらbhは3 ahは4だと思った Yahoo 知恵袋
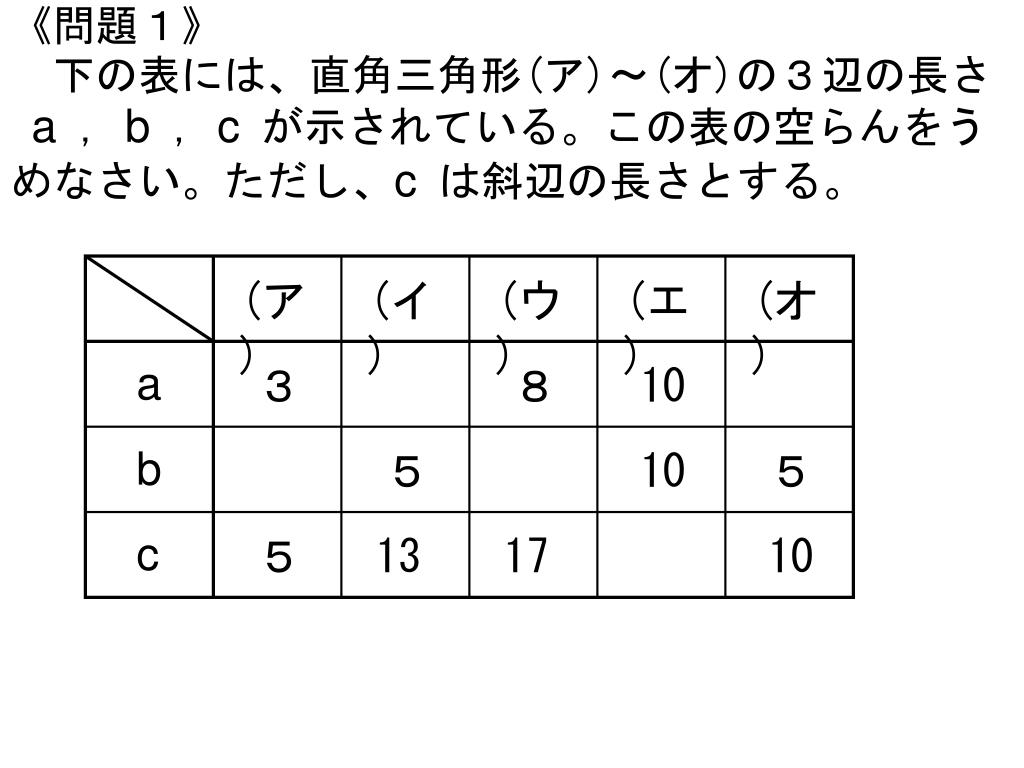



Ppt 6 三平方の定理 Powerpoint Presentation Free Download Id




Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三角比を用いた計算問題をマスターしよう スタディクラブ情報局



三平方の定理



三平方の定理の証明が種類以上載っているサイト 教えてください Yahoo 知恵袋



周髀算経 中国版 三平方の定理




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学
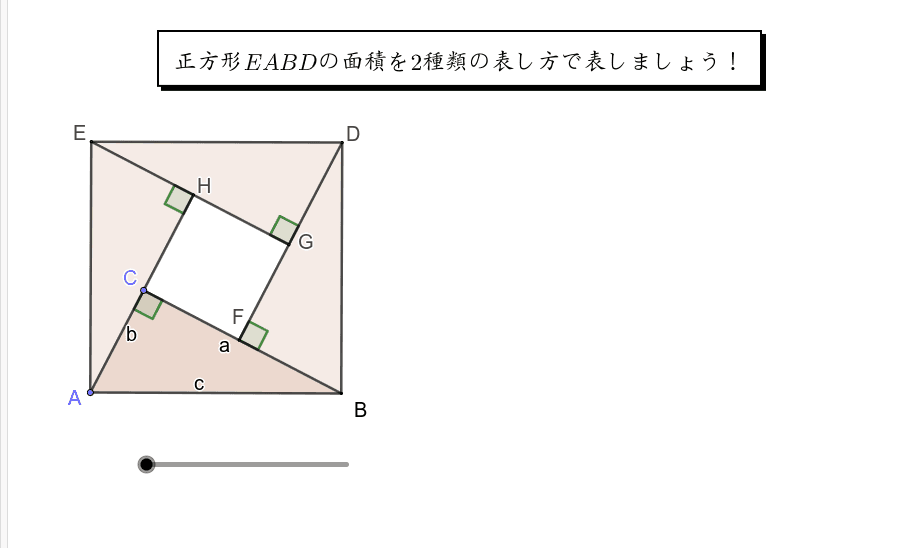



三平方の定理の証明 Geogebra




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学
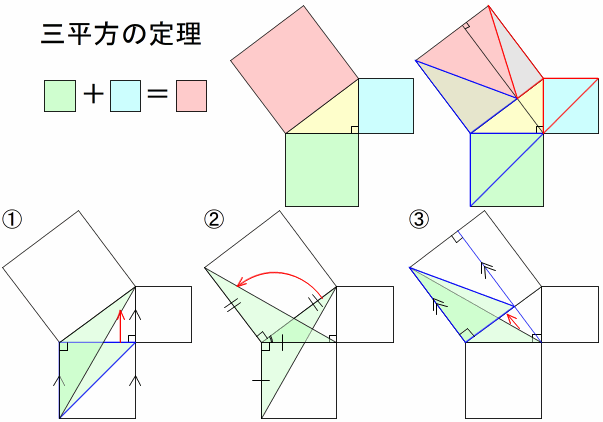



3 4 5の三角形で 本当に直角ができる Note Board




三角比 高校物理の備忘録




二個の平方数の和 Wikipedia
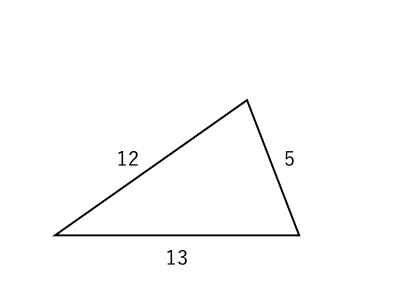



三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に



3
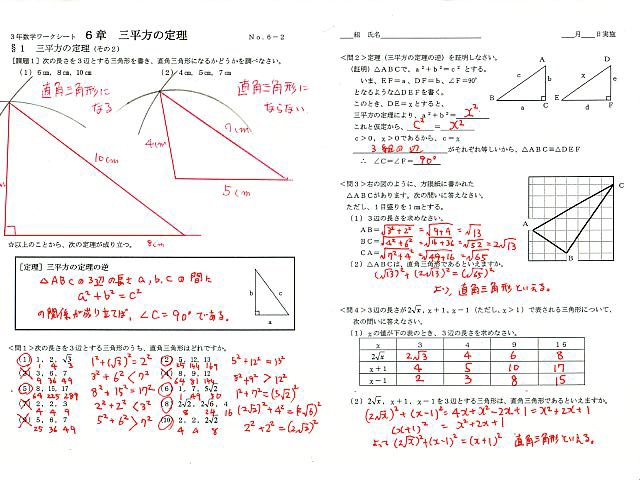



2 三平方の定理の逆 Mathweather4067のblog




この表のおぼえかたとかありますか Clear




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube



数学のコツ 三平方の定理 個別指導ソラオトのスタッフブログ



単位円とは 1分でわかる意味 覚え方 表 Sin Tanとの関係
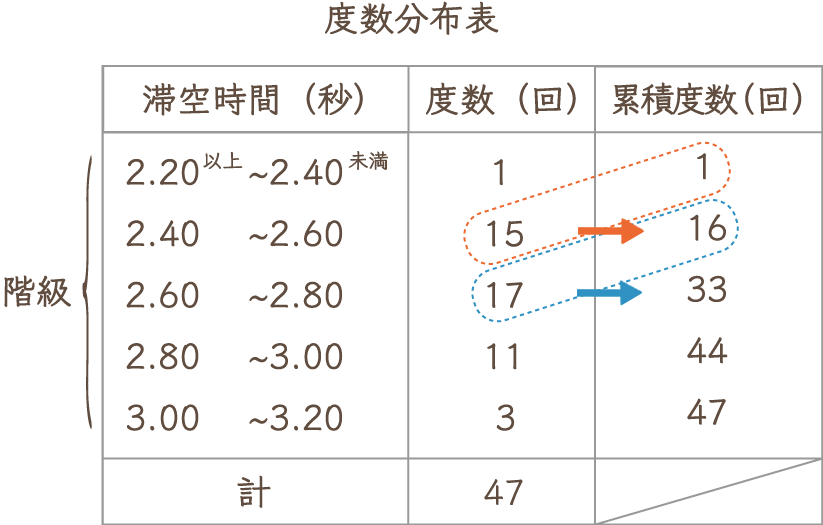



21年最新版 新しい中学数学はデータまみれ 累積度数や箱ひげ図などが新たに追加



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
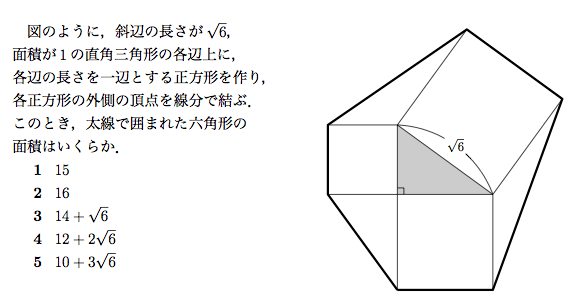



三平方の定理 二辺が等しく夾角が補角である三角形 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



0 件のコメント:
コメントを投稿